Grossièrement, une matrice est un tableau. Le problème est de savoir comment on va le remplir.

Généralités :

On note M_{n, p} (k) l'espace vectoriel des matrices à n lignes et p colonnes dont les coefficients sont dans k. Il est de dimension np.

On note a_ij le terme situé à la i-ème ligne et la j-ème colonne. Si A est la matrice de terme général a_ij, on écrit : A = (a_ij)_ij.

La base canonique de M_{n, p} (k) est (E_ij) où E_ij est la matrice ne contenant que des 0 sauf à la

i-ème ligne, j-ème colonne où il y a un 1 : A =

Propriétés :

Soit AÎ M_{n, p} (k), BÎ M_{p, q} (k). Le produit de A par B noté AB est un élément de M_{n, q} (k).

On suppose que la technique de calcul de ce produit est connue (sans faire d'erreur !).

Pour des matrices ayant le nombre de lignes et de colonnes nécessaires, on peut écrire :

(A + A')B = AB + A'B

C(A + A') = CA + CA'

(AB)C = A(BC)

AI = IA = A où I est la matrice identité (des zéros partout sauf sur la diagonale où il y a des 1).

Attention : AB = 0 n'entraîne pas A = 0 ou B = 0. (absence d'intégrité).

AB ¹ BA.

Proposition : M_n (k) = M_{n, n} (k) est une algèbre. Le groupe des inversibles est noté GL(n). Le neutre pour le produit est la matrice identité. On peut montrer que GL(n) est dense dans

M_n (k) (i.e. toute matrice carrée est limite d'une suite d'éléments de GL(n)).

Propriétés :

Si AÎ GL(n), AX = AY Þ X = Y

XA = YA Þ X = Y

Théorème :

A, BÎ M_n (k) tel que AB = I alors A, BÎ GL(n) et B = A^-1.

Si A, BÎ GL(n), ABÎ GL(n) et (AB)^-1 = B^-1A^-1.

Transposition :

La transposée de A, noté ^tA, est la matrice de M_{p, n} (k) : ^tA = (a_ji)_ji.

La transposition est une involution et ^t(AB) = ^tB . ^tA.

Si A = ^tA, A est dite symétrique.

Si A = - ^tA, A est dite antisymétrique.

Si AÎ GL(n), ^tAÎ GL(n) et (^tA)^-1 = ^t(A^-1).

Traduction matricielle des opérations élémentaires :

On définit les matrices suivantes :

- matrices de transvection : T_ij =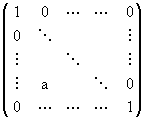où a est situé à la i-ème ligne,j-ème colonne.

- matrices de dilatation : D_i = 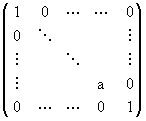où a est situé à la i-ème ligne,i-ème colonne.

- matrice de permutation : P_ij =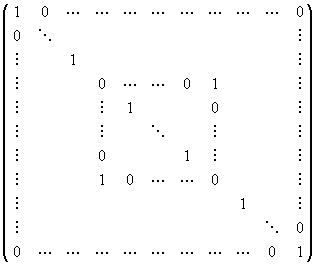

les 2 zéros de la diagonale étant à la i-ème et à la j-ième ligne.

Ces matrices sont utilisées notamment en algorithmique pour la résolution des systèmes linéaires.

f : E ® F

(e₁, ...,e_p) = B une base de E.

(e'₁, ..., e'_n) = B' une base de F.

La matrice de f entre B et B' appartient alors à M_{n, p} (k).

Elle est définit par : " jÎ [[1, p]], f(e_j) =

Exemple : f : r₃[X] ® r₂[X]

P ® P'

(1, X, X², X³) = B est une base de r₃[X].

(1, X, X²) = B' est une base de r₂[X].

matr_{B, B'} f =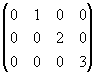

Application linéaire canoniquement associée à une matrice :

Si on prend 2 bases de bonne dimension et si A est une matrice, l'application linéaire canoniquement associée à A est l'application linéaire f dont entre la matrice entre ces 2 bases est A. La matrice et son application associée ont même rang, même noyau, même image, même valeurs propres et même vecteurs propres.

Propriétés :

- A est inversible si et seulement si f est un isomorphisme.

- la matrice de f o g est AB.

Enfin, on rappelle qu'une matrice commute avec toute matrice si et seulement si c'est une matrice scalaire i.e. une matrice de la forme aI i.e. une matrice d'homothétie.

Définition :

Une matrice A (resp. un endomorphisme f) est dite nilpotente si et seulement si il existe nÎ n tel que Aⁿ = 0 (resp. fⁿ = 0).

Définition :

Si on considère deux bases du même espace, la matrice de passage d'une base (l'ancienne) à l'autre (la nouvelle) est la matrice dont les colonnes sont les coordonnées des nouveaux vecteurs dans l'ancienne base.

Propriétés :

- une matrice de passage est inversible.

- si P est une matrice de passage, X un vecteur colonne représentant les coordonnées dans l'ancienne base et X' un vecteur colonne représentant les coordonnées dans la nouvelle base alors : X = PX'.

Formule de changement de base pour une application linéaire :

Soit f : E ® F

Soient B₁ et B₂ deux bases de E et B'₁ et B'₂ deux bases de F.

Soient P la matrice de passage de B₁ à B₂, Q la matrice de passage de B'₁ à B'₂, A₁ la matrice de f entre B₁ et B'₁ et A₂ la matrice de f entre B₂ et B'₂.

On a alors : A₂ = Q^-1 A₁ P. Dans le cas particulier des endomorphismes : A₂ = P^-1 A₁ P.

Matrices équivalentes :

On dit que A et B sont équivalentes si et seulement si $ P, Q inversible tel que : A = Q^-1 B P.

Deux matrices sont équivalentes si et seulement si elles représentent la même application linéaire par rapport à deux couples de base bien choisies.

Deux matrices sont équivalentes si et seulement si elles ont même rang.

Matrices semblables :

Dans M_n (k), on dit que deux matrices A et B sont semblables si et seulement si il existe P inversible telle que : B = P^-1 A P.

Remarque : semblable Þ équivalent.