Les Anneaux

I. Définitions
II. Eléments particuliers
III. Structures
IV. Morphismes
V. Les corps

I. Définitions

- Définition :

(A,+,*) est un anneau ssi

1. (A,+) est un groupe abélien
2. * est une loi de composition interne sur A, associative
3. * est distributive à droite et à gauche par rapport à +
4. * admet un élément neutre dans A

- Règles de calcul :

Soit (A,+,*) un anneau quelconque.

Eléments neutres :

On note 0_A l'élément neutre de la loi +, 1_A celui de la loi * (on note 0 et 1 lorsqu'il n'y a pas d'ambiguité possible).

x A , x * 0 = 0 * x = 0

Voir démonstration

Définition :

On appelle élément non nul de A tout élément de A distinct de 0_A.

Notation :

Pour tout élément x de A, on notera -x le symétrique de x pour la loi +.

Propriétés :

• (x,y) A² , (-x) * y = -(x * y) = x * (-y)
• (x,y) A² , (-x) * (-y) = x * y

Voir démonstration

Distributivité :

(a,b,c,d) A⁴ , (a + b) * (c + d) = a * c + a * d + b * c + b * d

Voir démonstration

- Multiplication entière et puissances :

Soit (A,+,*) un anneau quelconque

On pose:

x A , 0x = 0
x A , n N , (n +1)x = (nx) + x
x A , n N , (-n)x = -(nx)

et:

x A , x⁰ = 1
x A , n N , x^{n + 1} = (xⁿ) * x

Remarques :

1. On a également :
   • x A , n N , (n + 1)x = x + (nx)
   • x A , n N , x^{n + 1} = x * (xⁿ)

   Voir démonstration

2. En général, 0⁰ n'est pas défini; on peut poser ici 0⁰ = 1 mais des résultats de continuité peuvent aussi conduire à poser 0⁰ = 0 .

Propositions :

• x A , n Z , nx = (n1) * x = x * (n1)
• (x,y) A² , n Z , (nx) * y = x * (ny) = n(x * y)
• x A , (n,p) Z² , nx + px = (n + p)x

Voir démonstration

Notation :

(x,y) A² , n Z , nx * y = (nx) * y = x * (ny) = n(x * y)

Remarque :

Ces résultats n'interviennent pas dans la définition de l'anneau (Z,+,*).

Formule du binôme :

Soient a et b deux éléments de A tels que a * b = b * a
Alors :

Voir démonstration

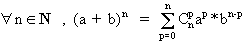
- Compléments :

Pseudo-anneau :

On appelle pseudo-anneau tout triplet (A,+,*) vérifiant les axiomes i, ii et iii:

1. (A,+) est un groupe abélien
2. * est une loi de composition interne sur A, associative
3. * est distributive à droite et à gauche par rapport à +

Remarque :

Ceci correspond à l'ancienne définition d'un anneau, la définition actuelle correspondant à la notion d'anneau unitaire.

Ancienne définition :

On appelle anneau tout triplet (A,+,*) vérifiant les axiomes i, ii et iii.

Ancienne définition :

On appelle anneau unitaire tout anneau vérifiant l'axiome iv (existence d'un élément unité).

Anneau commutatif :

Un anneau (A,+,*) est dit commutatif ssi la loi * est commutative sur A

Anneau nul :

Considérons l'ensemble {0}, muni des lois de composition internes + et * définies par:
0 + 0 = 0
0 * 0 = 0
Cet ensemble est un anneau (voir démonstration).
Il est appelé anneau nul.

Anneau unifère (ancienne définition) :

On appelle anneau unifère tout anneau unitaire non nul.

II. Eléments particuliers

- Diviseurs de zéro :

Soit (A,+,*) un anneau; soit a un élément non nul de A.

Définition :

On dit que a est diviseur de zéro à droite (resp. à gauche) ssi
b A\{0} , b * a = 0 (resp. a * b = 0).

Remarque :

Si (A,+,*) est un anneau commutatif, alors a est diviseur de zéro à droite ssi a est diviseur de zéro à gauche.

Voir démonstration

- Régularité :

Théorème :

a est régulier à droite (resp. à gauche) ssi il n'est pas diviseur de zéro à droite (resp. à gauche).

Voir démonstration

- Anneau intègre :

Définition :

Un anneau (A,+,*) commutatif et non nul est dit intègre ssi
(a,b) A² , (a * b = 0) (a = 0 ou b = 0)

Définition équivalente :

Un anneau intègre est un anneau commutatif non nul sans diviseurs de zéro.

Voir démonstration de l'équivalence

Théorème :

Soit (A,+,*) un anneau intègre; alors
a A\{0} , (x,y) A² , (a * x = a * y) (x = y)

Voir démonstration

- Eléments nilpotents :

Définition :

Soit (A,+,*) un anneau et soit a un élément de A.
a est dit nilpotent s'il existe un entier naturel n tel que aⁿ=0.
L'ensemble des entiers naturels n tels que aⁿ=0 est alors une partie non vide minorée de N; elle admet un plus petit élément, qui est appelé indice de nilpotence de a.

- Eléments idempotents :

Définition :

Soit (A,+,*) un anneau, et soit a un élément de A.
a est dit idempotent si a²=a

- Eléments inversibles :

Soit (A,+,*) un anneau quelconque; soit a un élément de A.

Définitions :

On dit que a est inversible à droite (resp. à gauche) dans A ssi
b A , a * b = 1 (resp. b * a = 1)
a est dit inversible dans A ssi a est inversible à droite et à gauche dans A.

Théorème :

Si a est inversible dans A, et si a * b = 1 (resp. b * a = 1), alors
b * a = 1 (resp. a * b = 1).

Voir démonstration

Théorème :

Si (A,+,*) est un anneau commutatif, tout élément de A inversible à droite ou à gauche dans A est inversible dans A.

Voir démonstration

Théorème :

Si a est inversible dans A, alors il existe un unique élément b de A tel que:
a * b = b * a = 1

Voir démonstration

On note cet élément b = a^-1.

Généralisation de la notion de puissance:

Si a est un élément inversible de A, alors on note:
n N , a^-n = (a^-1)ⁿ

On a ainsi défini aⁿ pour tout élément n de Z.

III. Structures

- Anneaux produits :

- Sous-anneaux :

Soit (A,+,*) un anneau; soit B une partie de A.

Définition :

On dit que (B,+,*) est un sous-anneau de A lorsque (B,+,*) est un anneau tel que 1_A soit l'élément neutre de * sur B.

Théorème :

Si (A,+,*) est un anneau intègre, et si (B,+,*) est un anneau, alors (B,+,*) est un sous-anneau intègre de (A,+,*).

Voir démonstration

- Idéaux :

La notion d'idéal a été introduite par Kummer pour ses travaux en arithmétique.

Soit (A,+,*) un anneau commutatif; soit I une partie de A.

Définition :

1. On dit que I est un idéal à droite (resp. à gauche) de A ssi
   • (I,+) est un sous-groupe de (A,+)
   • x I , a A , x * a I (resp. a * x I).
2. On dit que I est un idéal (ou idéal bilatère) de A ssi I est un idéal à droite et à gauche de A.

Proposition :

L'intersection d'une famille d'idéaux est un idéal.

Voir démonstration.

Définition :

• On dit que I est un idéal principal de A ssi I est un idéal de A engendré par un singleton, c'est à dire:
  i A , x I , a A , x = a * i
• L'anneau (A,+,*) est dit principal ssi tous ses idéaux sont principaux.

Proposition :

Si I est un idéal de A et si I contient un élément inversible de A, alors I=A.

Voir démonstration.

- Anneaux quotients :

IV. Morphismes

- Définitions :

Soient (A,+,*) et (B,T,o) deux anneaux; soit f une application de A vers B.

On dit que f est un morphisme d'anneaux ssi

1. (x,y) A² , f(x + y) = f(x) T f(y)
2. (x,y) A² , f(x * y) = f(x) o f(y)
3. f(1_A) = 1_B

- Noyau, image :

Définitions :

Soient (A,+,*) et (B,T,o) deux anneaux, et soit f un morphisme de A vers B.
• Le noyau de f est le sous-ensemble de A défini par f^-1(0_B); on le note Kerf.
• L'image de f est le sous-ensemble de B défini par f(A); on le note Imf.

Proposition :

Kerf est un idéal de A.

Voir démonstration.

Remarque :

(Kerf,+) est un sous-groupe de (A,+), donc il contient 0_A; donc f(0_A) = 0_B

- Propriétés :

Proposition :

Soient (A,+,*) et (B,T,o) deux anneaux, soit f un morphisme de A vers B.
f est injectif si et seulement si f(0_A) = 0_B.

Voir démonstration.

- Décomposition canonique:

V. Les corps

Définition :

On appelle corps un anneau dont tous les éléments non nuls sont inversibles.

Exemples :

Les anneaux Q, R, C sont des corps.

Proposition :

Soit (A,+,*) un anneau quelconque. A est un corps si et seulement s'il a exactement deux idéaux: A et {0_A}.

Voir démonstration.

Corollaire :

Soient (A,+,*) un corps et (B,T,o) un anneau quelconque, soit f un morphisme d'anneaux de A vers B.
Alors f est soit nul, soit injectif.