Pourquoi calculer Zêta(2) ?
Déjà parce que, en soit, c'est un résultat
étonnant que 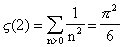
Ensuite parce que les démonstrations qui suivent
sont toutes des classiques, qu'il est utile de connaître,
en particulier pour ceux qui préparent les concours des
grandes écoles d'ingénieurs françaises :
ce sont des oraux classiques.
Puis, c'est un résultat mythe de mon ancienne
classe de sup 2....
Les méthodes font appels à des parties
très différentes des mathématiques, elles
brassent un ensemble de notion assez large.
II. Zêta de deux par la méthode
des polynômes
On part de l'étude des zéros du polynôme
complexe
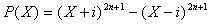
On note que X = i n'est pas solution : 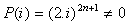 ,
on suppose donc X différent de i, et on écrit :
,
on suppose donc X différent de i, et on écrit :
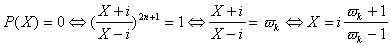
où 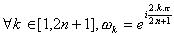 désigne
une racine (2n+1)-ième de l'unité.
désigne
une racine (2n+1)-ième de l'unité.
On a donc encore, en multipliant par 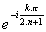 en haut et en bas :
en haut et en bas : 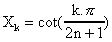 . Les solutions sont
toutes distinctes, on les a donc toutes par des considérations
de degré.
. Les solutions sont
toutes distinctes, on les a donc toutes par des considérations
de degré.
Repartons alors du même polynôme, et développons-le selon la formule du binôme.
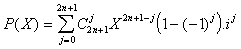
Si j est pair, alors le coéfficient est nul,
sinon, on peut factoriser : 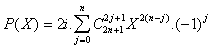
Maintenant si on pose 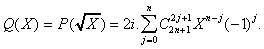 , on
sait que l'opposé du coéfficient de degrès
n-1 du polynôme normé est la somme des solutions
de Q(X), ie :
, on
sait que l'opposé du coéfficient de degrès
n-1 du polynôme normé est la somme des solutions
de Q(X), ie :
Ourvrir le cours sur les polynômes (non encore
fait !)
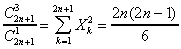
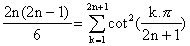
or on a l'inégalité : sin(x)<x<tan(x)
donc, 1/x > cotan(x) d'une part et x>sin(x) donc
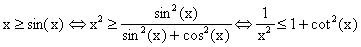
Finalement : 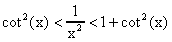
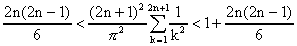
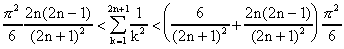
Lorsque on fait tendre n vers plus l'infini, les
deux suites à gauche et à droite convergent vers
la même valeur, on peut donc conclure que Zêta(2)
existe et vaut : 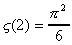
III. Zêta de deux par la méthode
des séries de Fourrier
Ouvrir le cour sur les séries de Fourrier
(non encore fait..)
On étudie la fonction continue, 2-périodique,
dont la restriction sur [-,+] coïncide avec la fonction valeur
absolue.
La fonction est donc paire, les coefficients bn de Fourrier sont donc nuls, le calcul des coefficients an donne :
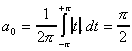
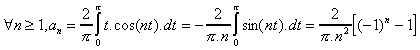
donc pour n paire, le coefficient est nul.
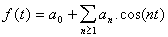
On en déduit :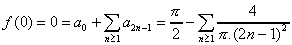
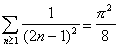
On observe alors que : 1
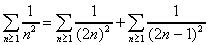
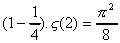
On aboutit donc au résultat suivant :
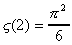
Cette méthode se généralise
bien. Cela est fait dans l'article suivant :
Ouvrir l'article sur le calcul de Zêta pour les entiers pairs
IV. Zêta de deux par la méthode
des intégrales
Euh ?? C'est bête hein ? Je m'en
rappelle plus... A venir prochainement, le temps que je rassemble
mes idées la-dessus. (c'est assez bourrin, si je me rappelle
bien)
Je vous dirai bien d'aller voir en attendant le cour
sur les intégrales, mais il n'y en a pas encore :-)
...