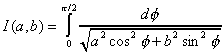
I. Introduction
- Définition
- Autre expression de l'intégrale elliptique de premier ordre
- Autre expression de l'intégrale elliptique de second ordre
II. Apparition des intégrales elliptiques
- Période d'un pendule
- Une intégrale apparemment simple
- Périmètre de la lemniscate
- Périmètre d'une ellipse
- Longueur d'une sinusoide
III. Simplification des intégrales elliptiques
- Cas triviaux
- Combinaison avec la moyenne aritmético-géométrique
- Relation entre I et J
IV. Développement sur les intégrales elliptiques

I. Introduction

- Définition

Les intégrales elliptiques sont de deux sortes.

L'intégrale elliptique du premier ordre I est définie pour 0 < b < a

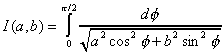
L'intégrale elliptique du second ordre J est définie pour 0<b<a

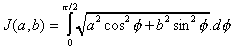
Ces intégrales ne sont pas résolubles pas les moyens habituels. Néanmoins, on sait en dire quelques chose.

On définit aussi L(a,b), qui nous sera très utile pour étudier les intégrales elliptiques

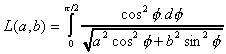
- Autre expression de l'intégrale elliptique de premier ordre

Par exemple, opérons le changement de variable 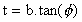sur I(a,b)

Comme 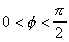, c'est bien un R-difféomorphisme, donc un changement de variable.

On a alors

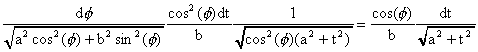
or on a :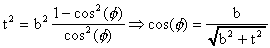

et donc (par parité de la fonction sous le signe somme) :

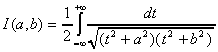
- Autre expression de l'intégrale elliptique de second ordre

De même, opérons le changement de variable 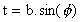sur J(a,b)

Comme , c'est bien un R-difféomorphisme, donc un changement de variable.

Ça donne a peu près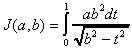, mais c'est vraiment pas sur, faudrait que

je regarde un de ces quatre. :-)

II. Apparition des intégrales elliptiques

Ce chapitre a pour rôle de montrer comment sont apparues ces intégrales dans l'histoire des mathématiques et de la physique.

- Période d'un pendule

Il s'agit de résoudre exactement le calcul de la période d'oscillation d'une masse m attachée au bout d'un fil inextensible de longueur l. On néglige tous les frottements.

Le pendule a une amplitude de 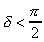. Soit P, le point maximum atteint par le pendule, et Q, le point courant (angle théta). La conservation de l'énergie entre P et Q nous donne la relation :

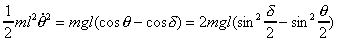
Pour calculer la période, on cherche a calculer

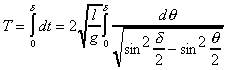
On opère alors le changement de variable 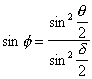, qui nous montre que

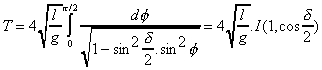
Ce qui montre que la période exacte n'est pas calculable avec les outils traditionnels, et explique qu'on ne résolve jamais exactement la période d'un pendule.

(rappel : les physiciens opèrent un développement limité)

- Une intégrale apparemment simple

Un des problèmes qui furent posés aux cours des siècles au mathématiciens fut de calculer l'intégrale . Pour qui connaît ses dérivées usuelles, le cas n=2 est trivial. Beaucoup plus dur est le cas n=4, en effet le changement de variable 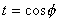nous montre que

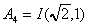
Ce qui nous permet d'affirmer que cette intégrale n'est pas résoluble avec les fonctions usuelles.

- Périmètre de la lemniscate

La lemniscate de Bernoulli est la figure qui a donné naissance au signe infini. Elle a pour équation polaire

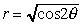
Par définition, le périmètre de la lemniscate est donc de :

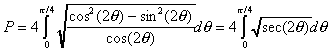
Le changement de variable nous montre alors que 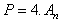, (voir question précédente), et que donc, on se retrouve encore ici avec une intégrale elliptique.

- Périmètre d'une ellipse

Il est paradoxale de voir a quel point l'aire d'une ellipse généralise très bien l'aire d'un cercle, tandis que son périmètre, comme nous allons le voir, se rapporte à une intégrale elliptique.

L'ellipse, comme chacun sait, et la courbe dont les points vérifient l'équation x²/a²+ y²/b²=1 , que l'on peut paramétrer par (a.sin(), b.cos()), de telle manière que

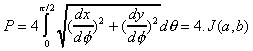
Bien entendu, j'imagine que c'est de cet exemple que vient le nom d'intégrale elliptique.

- Longueur d'une sinusoide

La longueur d'une sinusoide y=sin(x), est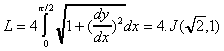

III. Simplification des intégrales elliptiques

- Cas triviaux

On a évidemment :

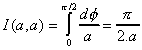
- Combinaison avec la moyenne aritmético-géométrique

La combinaison de la moyenne de Gauss et des intégrales elliptiques du premier ordre donne un résultat étonnant.

Ouvrir l'article sur la moyenne de Gauss

Soit donc a et b deux réels vérifiant 0<b<a. On cherche à calculer l'intégrale elliptique associée a un couple (a_n+1,b_n+1) de la suite arithmético-géométrique.

Soit donc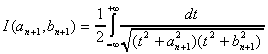

On opérant le changement de variable 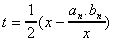qui donne

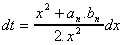
on a alors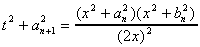

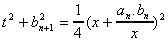
ce qui nous donne :

On a donc, nN 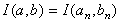, et par continuité

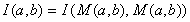
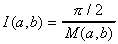
Ce résultat fondamental nous permet de calculer les intégrales elliptiques aussi rapidement que les moyennes arithmétiques.

- Relation entre I et J

Le changement de variable 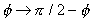sur la fonction L(a,b) nous montre que

On obtient donc la relation L(a,b)+L(b,a)=I(a,b), qui est l'intérêt de cette fonction L.

L'article sur Gauss-Salamin nous montre la formule suivante

où 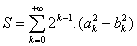, et

Les suites a et b étant les suites définit pour calculer la moyenne arithmético-géométrique, ou moyenne de Gauss, qui fait également l'objet d'un article.

Ouvrir l'article sur l'algorithme sur Gauss-Salamin

Ouvrir l'article sur la moyenne de Gauss

Tout cela est très lié, mais ne méritait pas un seul article pour tout.

On a alors :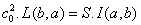

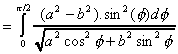
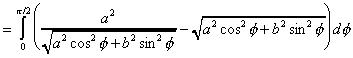
= a². I(a,b)- J(a,b)

IV. Développement sur les intégrales elliptiques

Elles sont utilisées dans un algorithme pour calculer pi avec beaucoup de décimales, article auquel j'ai déjà fait allusion.

Ouvrir l'article sur l'algorithme de Gauss-Salamin